平行四辺形の対角線の性質 241050-平行四辺形の対角線���性質

 証明問題②「平行四辺形とひし形の対角線」 ベクトルの平行条件「\(\vec{a} = k\vec{b}\)」 \(2\) つのベクトルが平行であるための条件を「ベクトルの平行条件」といいます。平行4辺形の対角線はそれぞれの中点で交わるので ・ ・ ・ ① ①より と は2等辺3角形なので よって、 ・ ・ ・ ② 4角形 において ① ② より 対角線がそれぞれの中点で交わるので 4角形 は平行四辺形次の各性質がつねに成り立つ図形に を付けなさい． （※この問題では，成り立つものはすべて ，成り立たないものはすべて としたときだけが正答となり，1つでも間違っていると正答とはなりません．各々6個のチェックボックスが完全に合っていなければ正答とはなりませんので，大変難しい

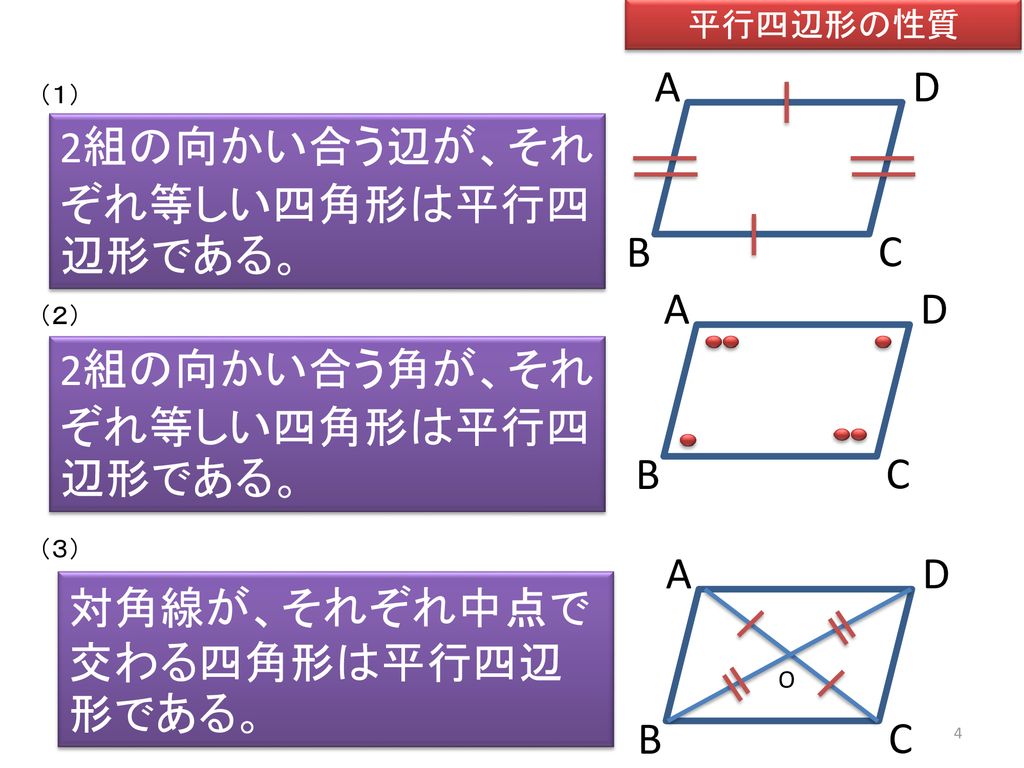
平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

平行四辺形の対角線の性質

平行四辺形の対角線の性質-平行四辺形に対角線を引くと、2つの対角線が交わる点が、それぞれの対角線の中央にきます。 上記は平行四辺形の性質なので、是非理解しましょう。 平行四辺形の面積 平行四辺形の面積は、 底辺×高さ で計算します。下図のように、平行四辺形に垂直線 四角形の対角線が中点でまじわっているとき だ。 これも平行四辺形の性質の逆さ。 たとえば、 四角形abcdの対角線を2本ひいたとき、 対角線acとbdがmでまじわっているとしよう。 このとき、もし、 am = cm = 6 cm;

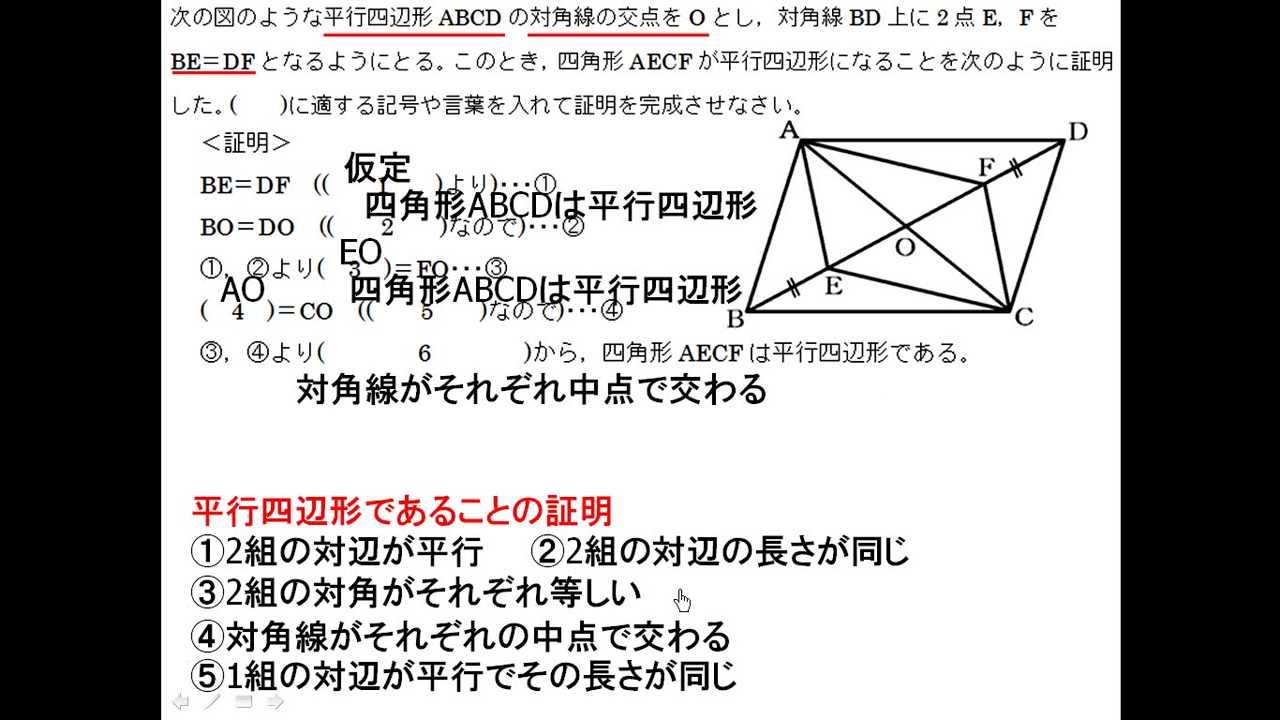
中2 数学 5 3 平行四辺形の証明 Youtube

平行四辺形の定義と性質をまとめると以下の通り。 平行四辺形の定義と性質 定義 向かい合う2組の辺がそれぞれ平行な四角形 定理（性質） 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 定義は 「こういう4 平行四辺形の性質を利用する証明問題 問題2 図のように，平行四辺形abcdの対角線ac上にae=cfとなるように，2点e，fをとる。このとき，be=dfであることを証明しなさい。 問題の見方 平行四辺形という条件から，次の3つの性質が活用できます。形の対角線の性質を統合的にとらえたりすることができる。 技能 ・垂直な2 直線や平行な2 直線及び，台形，平行四辺形，ひし形をかくことができる。 知識・理解 ・垂直な2 直線や平行な2 直線及び，台形，平行四辺形，ひし形の意味や性質につい

辺と対角線のある平行四辺形の領域をどのように見つけますか？ The area of a parallelogram can be calculated when the diagonals and their intersecting angle are known The formula is given as, area = ½ × d1 × d2 sin (x) , where 'd1' and 'd2' are lengths平行四辺形では、対角線を引くと それぞれの中点で交わります。 厳選6パターンの問題に挑戦！ それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基現時点では，平行四辺形では2組の対辺がそれぞれ平行であるしか使えません． そこから，平行四辺形の性質を学んでいくことになります． 命題1 平行四辺形は，2組の対辺がそれぞれ等しい． 証明 abcと cdaにおいて ac＝ca ab∥cdより ∠a＝∠c ad∥bcより

平行四辺形の定義は、「\(\boldsymbol{2}\) 組の向かい合う辺が平行な四角形を平行四辺形という 」になります。また、平行四辺形になるためには、定義を含めて \(\boldsymbol{5}\) つの条件 があります。平行線の錯角は等しいので∠oab=∠ocd, ∠oba=∠odc 平行線の対辺は等しいので、ab=cd よって1組の辺とその両端の角がそれぞれ等しいので aob≡ cod 合同な図形の対応する辺は等しいのでao=co, bo=do よって平行四辺形の対角線はそれぞれの中点で交わる 対角線の性質 対頂角は等しい 平行線の性質 2つの直線が平行ならば、同位角は等しい。 2つの直線が平行ならば、錯覚は等しい。 三角形の内角の性質 三角形の内角の和は180°である。 参考 中2数学（正）多角形の角度 三角形の外角の性質

平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

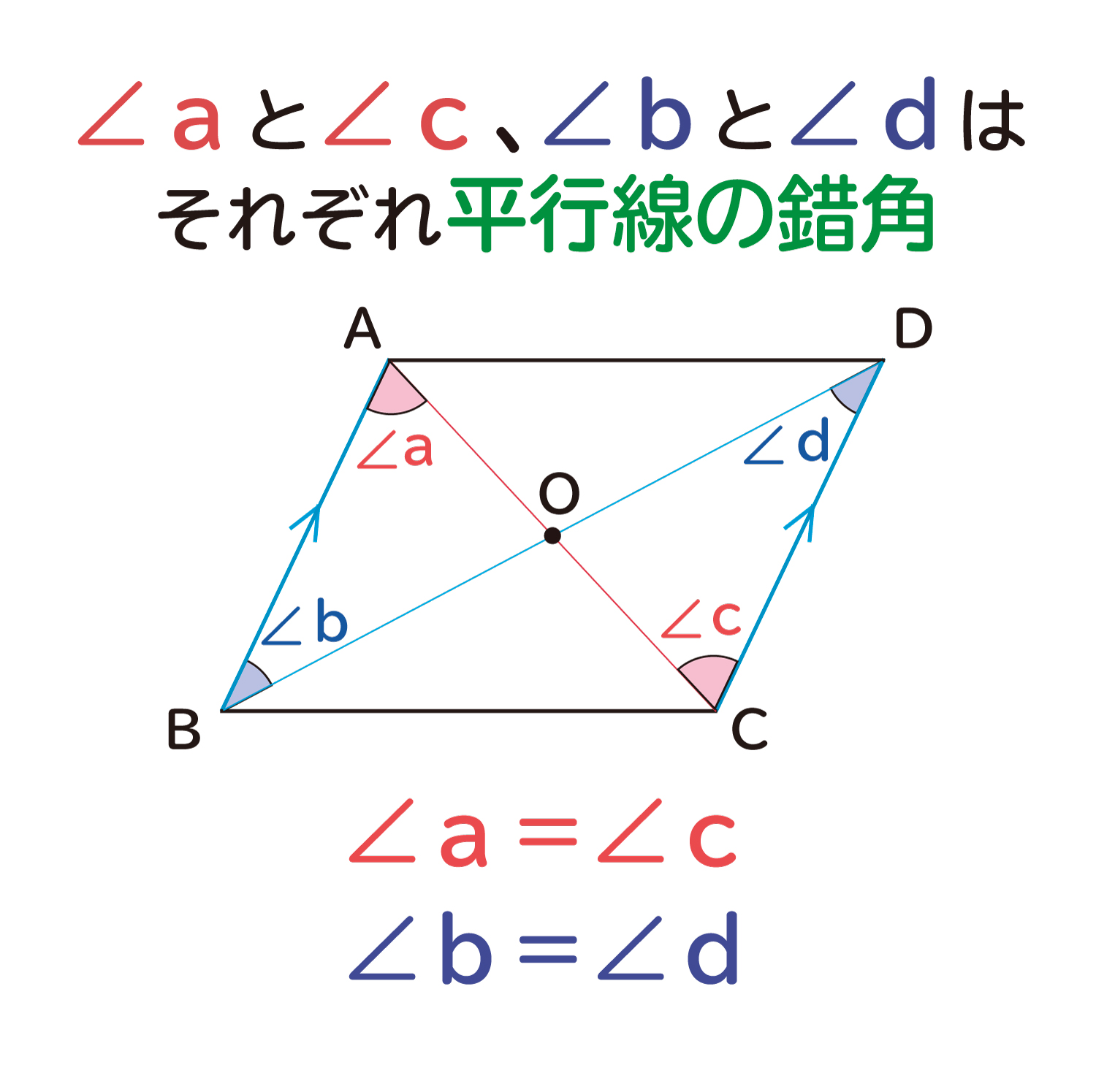
平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

平行四辺形の性質について学んだあと、どのように証明問題を解けばいいのか解説していきます。 もくじ 1 平行四辺形の定義と4つの性質 11 2組の対辺の長さが等しい 12 2組の対角がそれぞれ等しい 121 対辺と対角が等しい証明 13 隣り合う角度を足す 「テスト範囲をまとめました！ 練習問題も入れたので見ていただけたら嬉しいです🤍」, 学年 中学全学年, キーワード 数学,直角三角形,合同,証明,平行四辺形,台形,ひし形,正三角形,長方・平行四辺形には、下のような3つの性質があります。 1．対辺の長さが等しい 2．対角の角度が等しい 3．対角線は中点で交わる 今回、1つ目の平行四辺形の性質である、 対辺の長さが等しい ことを確認していきたいと思います。

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

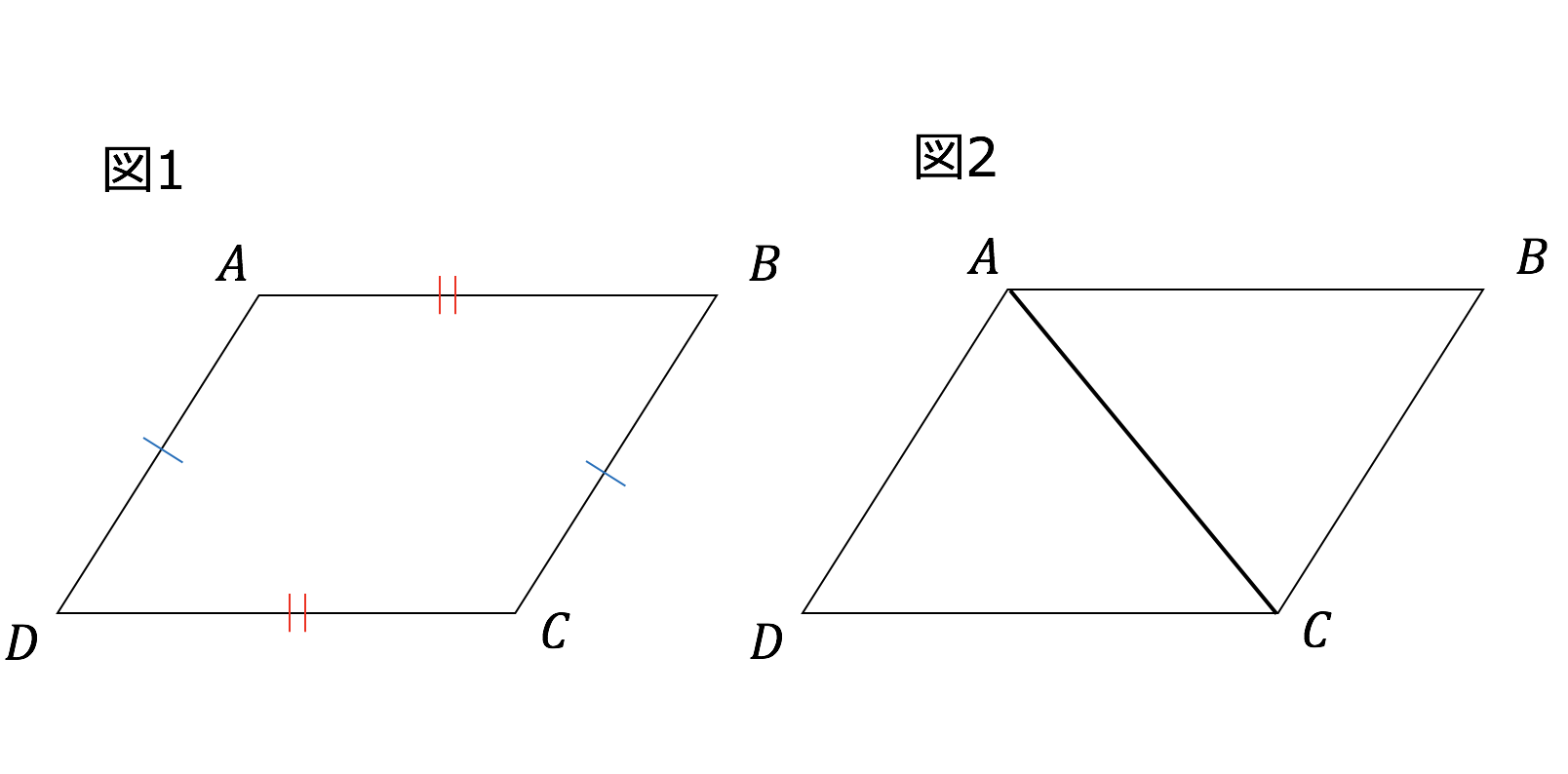
3分で分かる 平行四辺形とは 定義や性質 成立条件をわかりやすく 合格サプリ

 平行四辺形の性質（定理） ① 組の向かい合う辺の長さが等しい ② 組の向かい合う角が等しい ③ 本の対角線が中点で交わる 言葉だけで覚えるのは難しいと思うので、図とともに理解しながら覚えておきましょう。5．平行四辺形の性質 ★平行四辺形 定義 2組の向かい合う辺が，それぞれ平行な四角形 性質 (1)2組の向かい合い辺は，それぞれ等しい。 （定理）(2)2組の向かい合う角は，それぞれ等しい。 (3)対角線は，それぞれの中点で交わる。 (1) (2) (3)(1組の辺とその両端の角) がそれぞれ等しいから, abc≡ cda よって, ab＝cd , bc＝da 2 性質3平行四辺形の対角線は,それぞれの中点で交わる 証明3 aboと cdoにおいて,

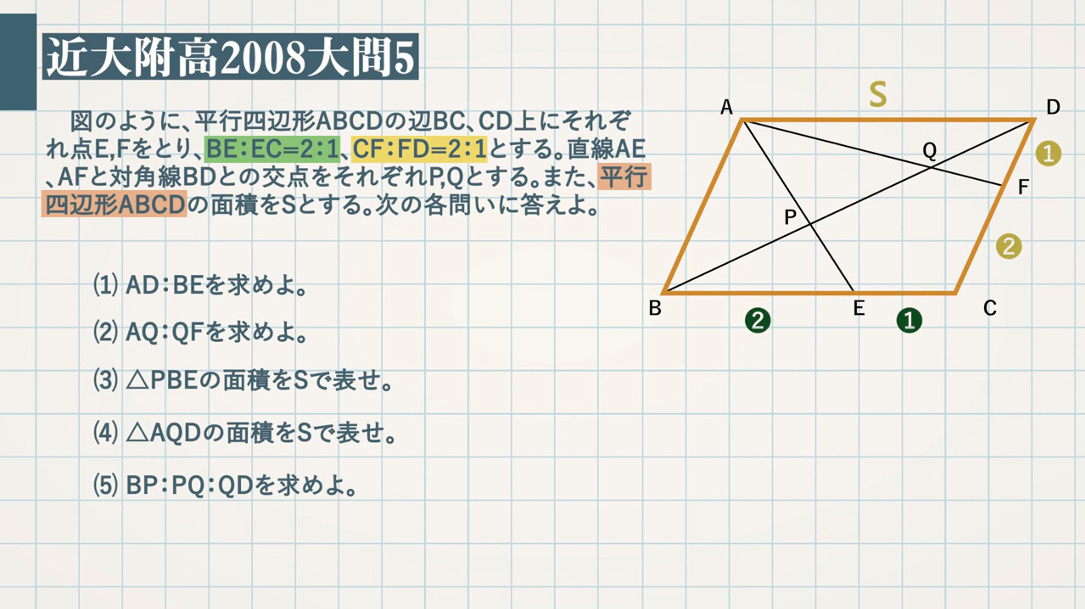
平行四辺形と比 教遊者

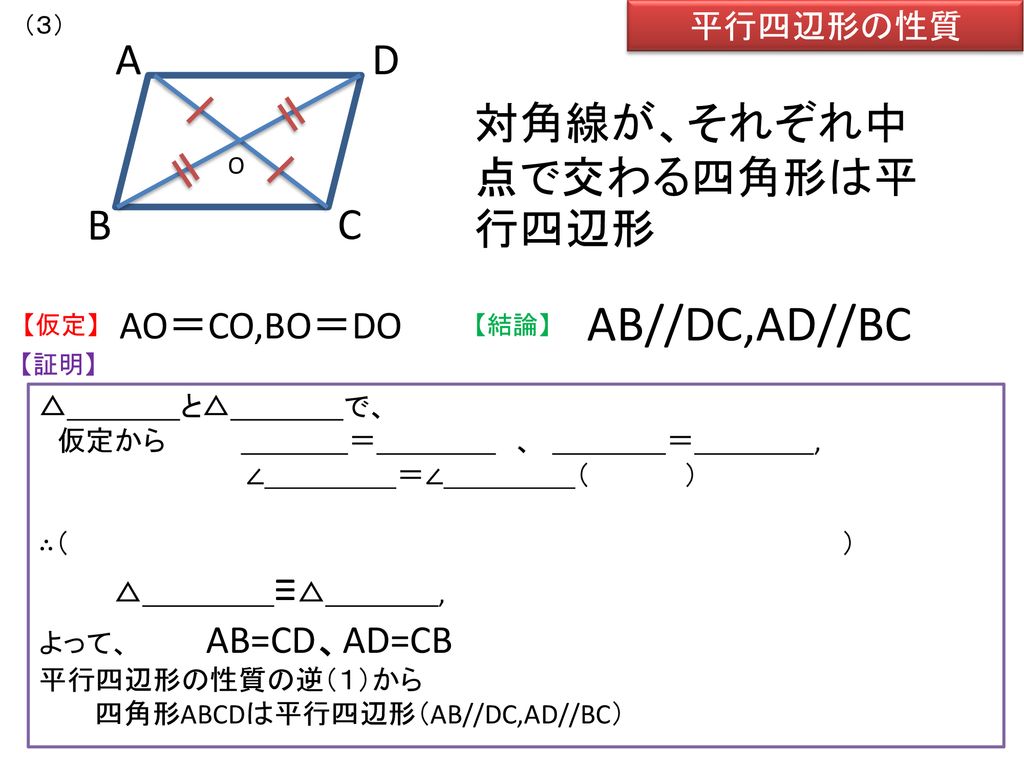
平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

平行四辺形の定義は 「2組の対辺が、それぞれ平行である四角形」 平行四辺形の定理 1 平行四辺形の2組の対辺は、 それぞれ等しい。 2 平行四辺形の2組の対角は、 それぞれ等しい。 3 平行四辺形の対角線は、 それぞれの中点で交わる。 1 2組の対辺が平行四辺形では、対角線はそれぞれの中点で交わる。 問題に出てくる平行四辺形に対角線が引かれていれば、この性質を利用する可能性がぐっと高まりますね。 それでは、以上の性質を頭に入れた上で証明問題を見ていきましょう。 問題に挑戦！ 中1 rimi 数学 平行四辺形の性質 証明 math この著者の他のノートを見る このノートが参考になったら、著者をフォローをしませんか？ 気軽に新しいノートをチェックすることができま

中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット

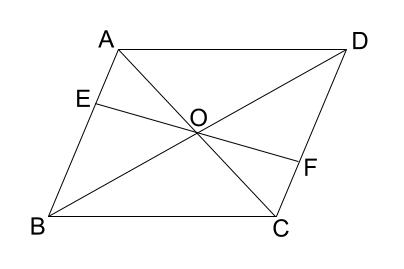
中学数学 証明 平行四辺形の性質の利用 中学数学の無料オンライン学習サイトchu Su

Abcdの対角線の交点oを通る直線が 辺ad tbcと交わる点をそれぞれ m t nとする このとき mo＝noであることを証明 しなさい z証明 { aomと conにおいて 平行線の錯角は等しいからad//bcより ∠mao＝∠nco・・・① 平行四辺形の対角線はそれぞれの中点で交わるからその等しい辺や角を、平行四辺形の定義をもとに証明していきます。 Ⅰ．2組の向かい合う辺や角が等しいことを証明。これは、平行四辺形の性質となる。 対角線ac をひく(元の図にない線なので記載する) abc と cda において ad // bc より平行線の錯角は等しい上の性質3を,記号で表しなさい。 oa ob 5 右の abcdについて,次の問いに答えなさい。 6 abcdに対角線を引くとき,合同な三角形を4組を見つけて,対応をつけて記号で答えなさい。 (1) 辺や対角線の長さを求めなさい。 辺ab＝ 辺bc＝ 対角線ac＝ (1)

相似 平行四辺形と面積比の問題を徹底解説 数スタ

Math 平行四辺形 平行四辺形になることの証明 働きアリ

 平行四辺形の性質 2組の対辺がそれぞれ等しい。 2組の対角がそれぞれ等しい。 対角線がそれぞれの中点で交わる。 つまりは平行四辺形は点対称だということだ。点対称とは180度回転しても合同な図形だと言うことだから、上の性質では3番が本質だといえる。Bm = dm = 8 cm;長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する

平行四辺形abcdの対角線の交点をｏとして 対角線bdにoe ｏｆとなる2 中学校 教えて Goo

平行四辺形の角の二等分線

平行四辺形の性質を利用した証明 ao=co (平行四辺形の対角線はそれぞれの中点で交わる) ∠aoe=∠cof (対頂角) ∠eao=∠fco (ab//cd 錯角) 1組の辺とその両端の角がそれぞれ等しいので aeo≡ cfo 合同な三角形の対応する辺は等しいので ae=cf

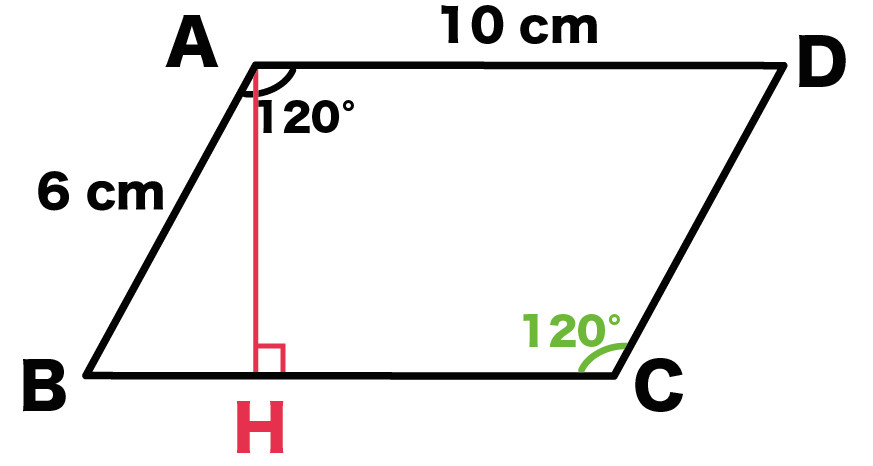
平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

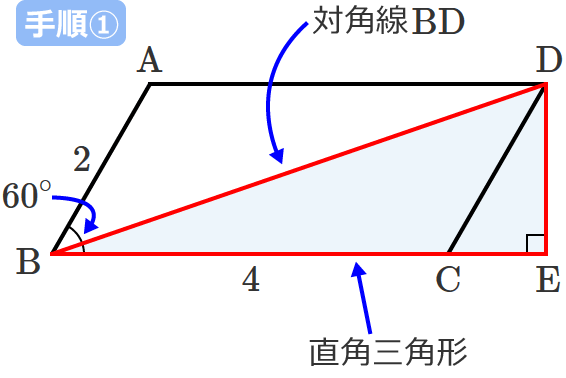
平行四辺形の対角線の長さの求め方

平行四辺形の性質

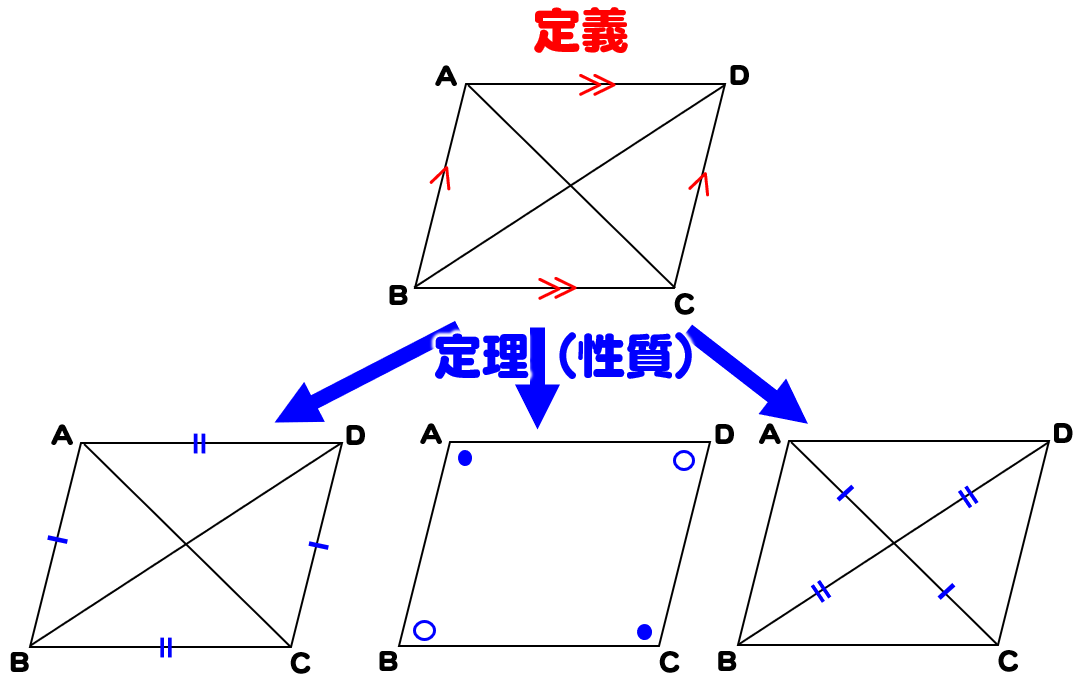
平行四辺形の定義と性質 証明問題の解き方 数学fun

無料 中２数学 基本解説 解答プリント 230 平行四辺形１ 性質

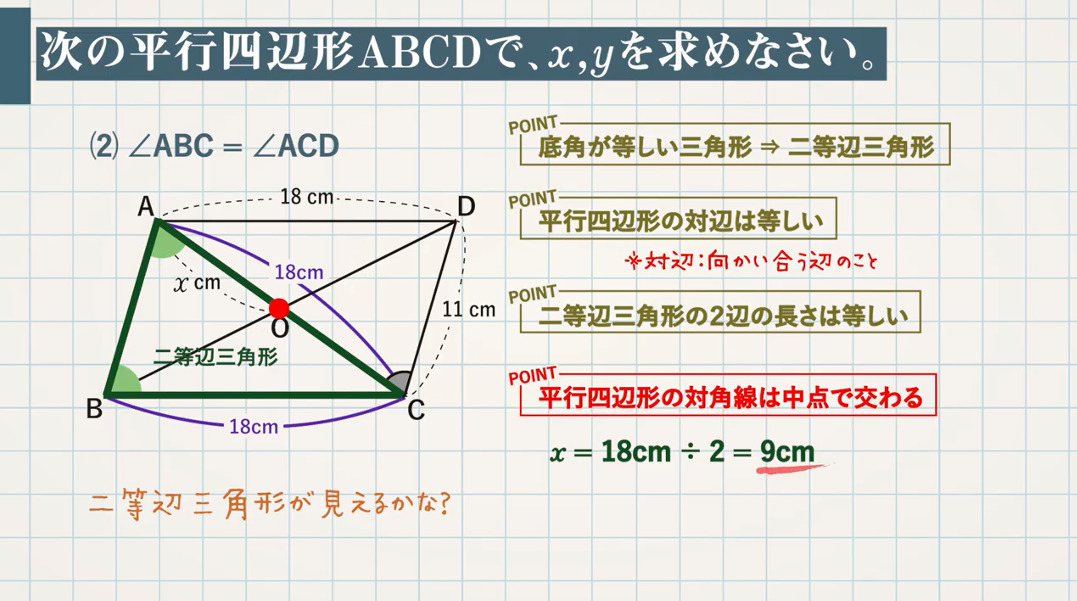
平行四辺形 二等辺三角形の辺の長さと角 応用問題まとめ 教遊者

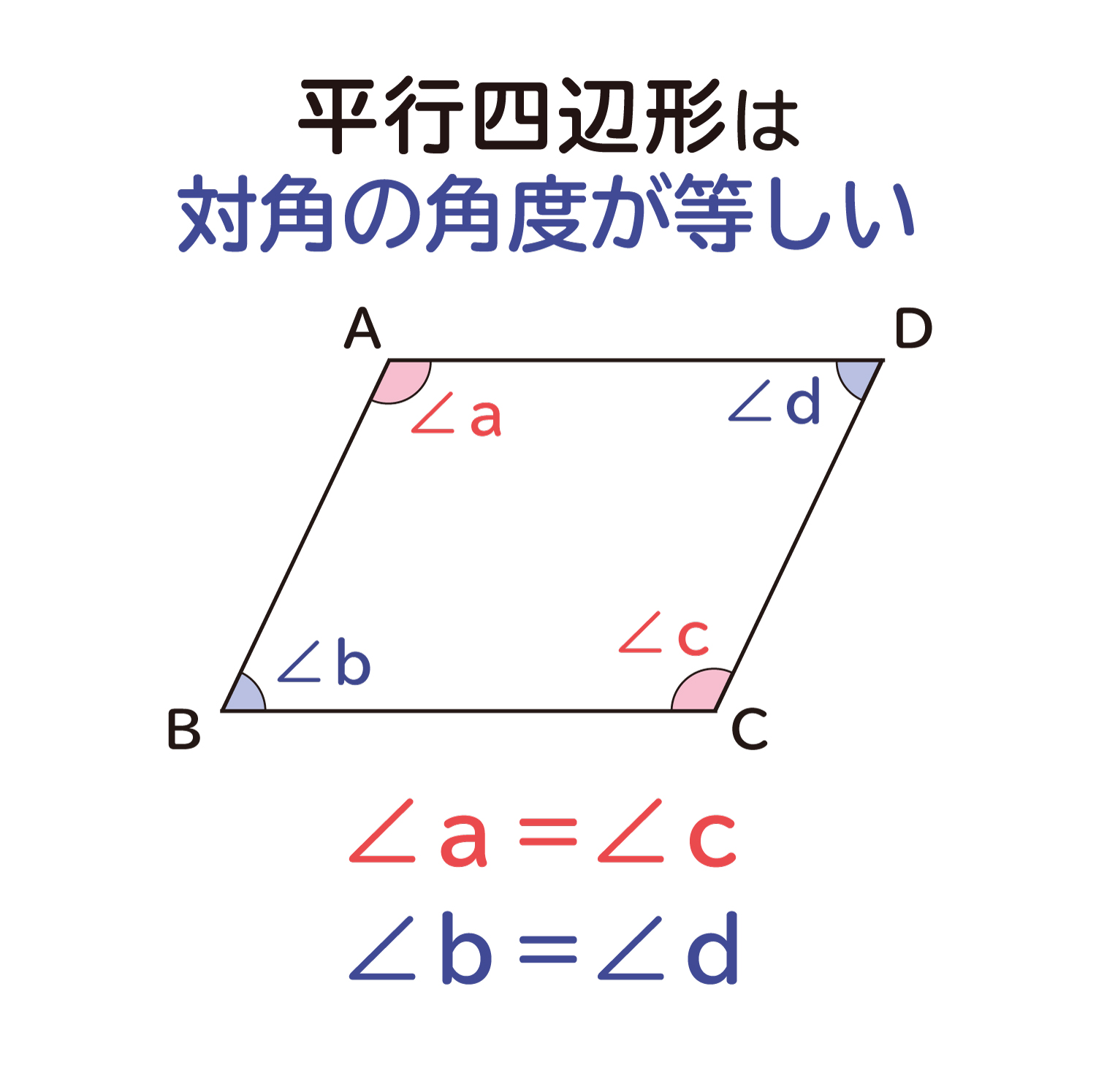
平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

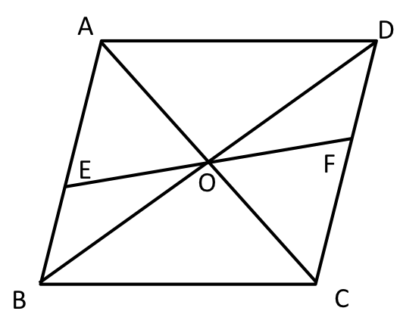
フロー 2 5 5 2 平行四辺形の性質を利用した証明

平行四辺形の対角線の交点を頂点とする三角形の面積 Okwave

平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室

証明分かりません 教えてください Clearnote

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

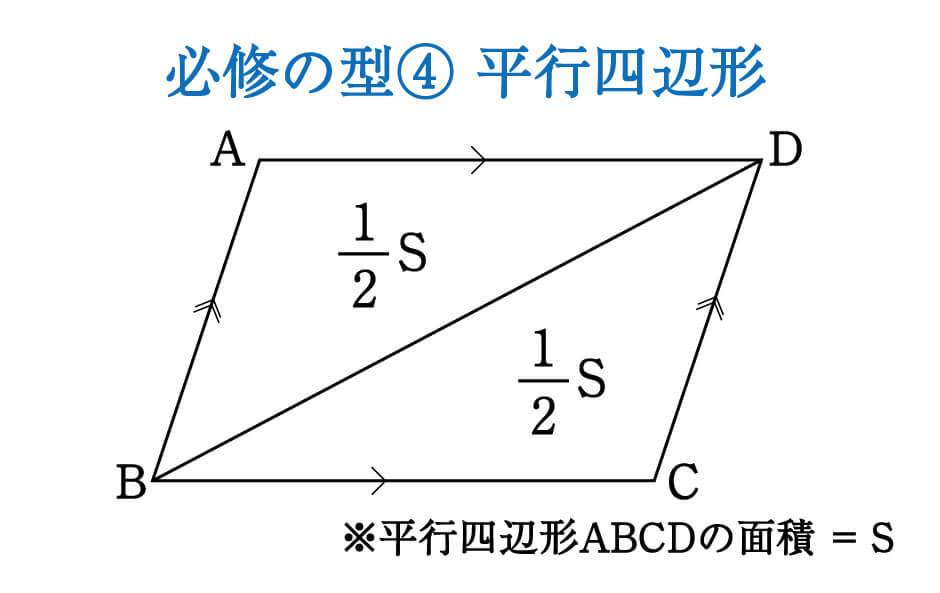
数学 面積比は全体から攻めると求めやすい 面積比 集中特訓 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

平行四辺形の定義と性質 証明問題の解き方 数学fun

平行四辺形の対角線の長さの求め方

平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ

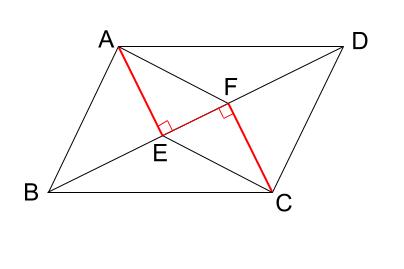
中学数学 平行四辺形になることの証明 その２ 中学数学の無料オンライン学習サイトchu Su

対角線で参観 教育考現学

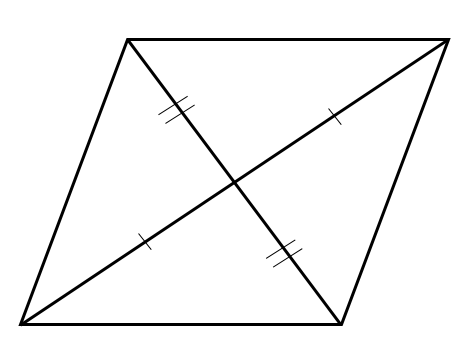
平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ

四角形 Ict教材eboard イーボード

平行四辺形の対角線の長さの求め方

定義と定理 12月 年 光が丘中学校 ブログ 光が丘中学校

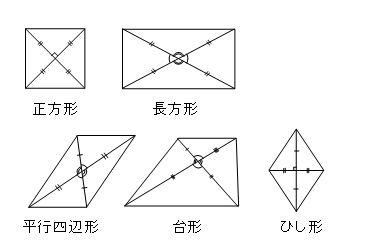
四角形の対角線 レッツスタディー

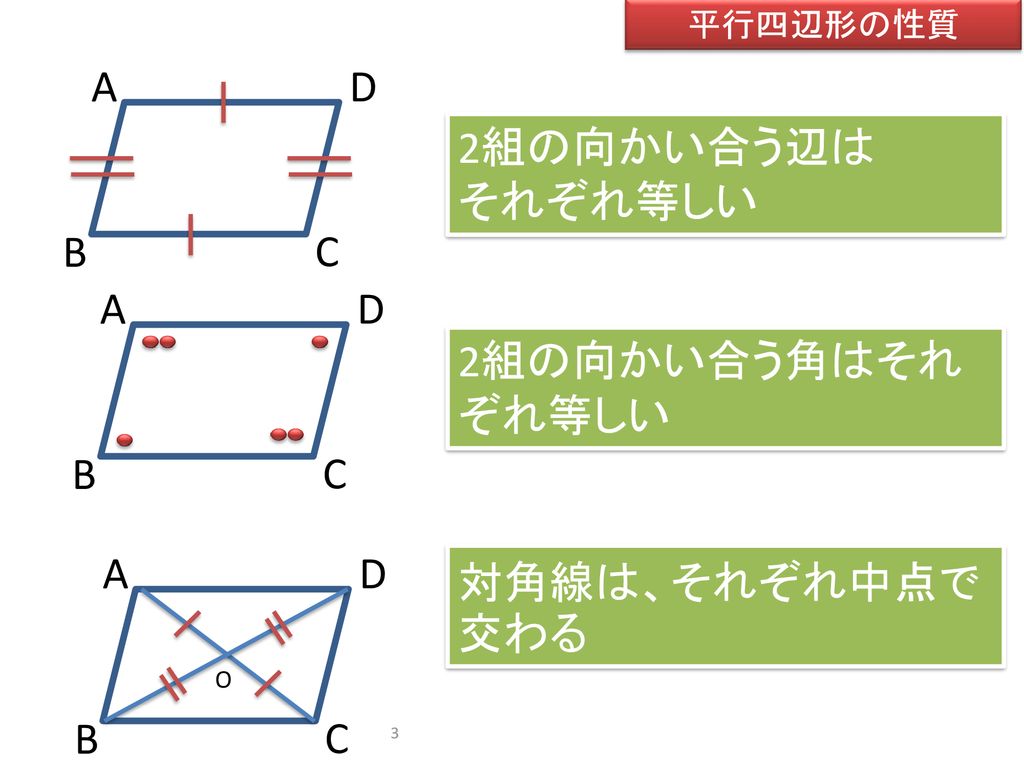
平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

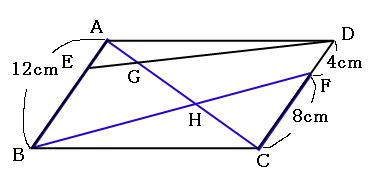
平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ

平行四辺形で知っておくべきこと 苦手な数学を簡単に

いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ 学習ノート 学習 小学校 算数

平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学

平行四辺形の性質の逆 四角形が平行四辺形になる条件 Ppt Download

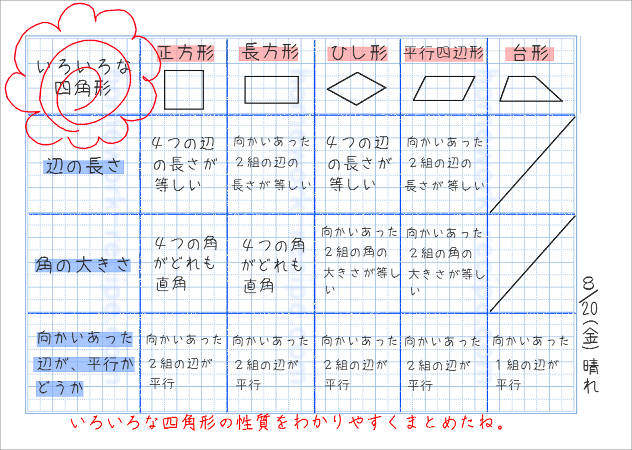
いろいろな四角形の性質をノートにまとめよう 家庭学習レシピ

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

平行四辺形対角線の求め方と面積について 対角線ａｃの長さの Yahoo 知恵袋

平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

中2 数学 5 3 平行四辺形の証明 Youtube

平行四辺形の性質の証明

四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ

3

1

４年算数 垂直 平行と四角形３ひし形の教え方

平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典

平行四辺形 Wikipedia

平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

平行四辺形の定義と性質 証明問題の解き方 数学fun

1

平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室

平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典

菱形定義 平行四辺形 ひし形 長方形 正方形の違い Vsrius

中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット

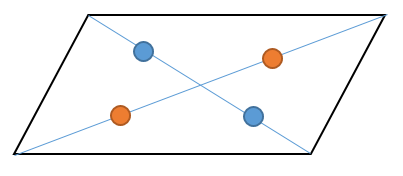
小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー

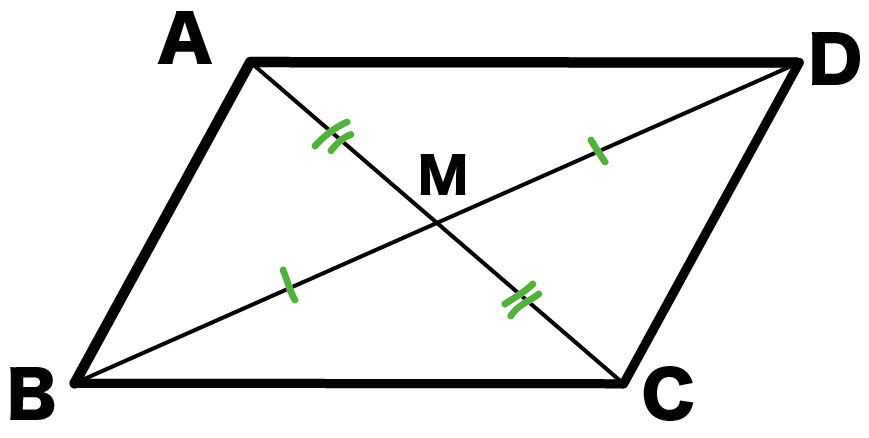
中2数学 平行四辺形の性質がわかる3つの証明 Qikeru 学びを楽しくわかりやすく

４年算数 垂直 平行と四角形３ひし形の教え方

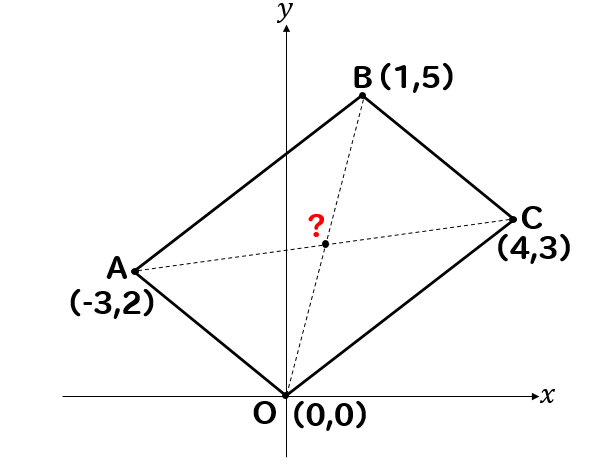
関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ

1

テボールの定理 雑学のソムリエ

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

平行四辺形の性質

標準 平行四辺形とベクトルの演算 なかけんの数学ノート

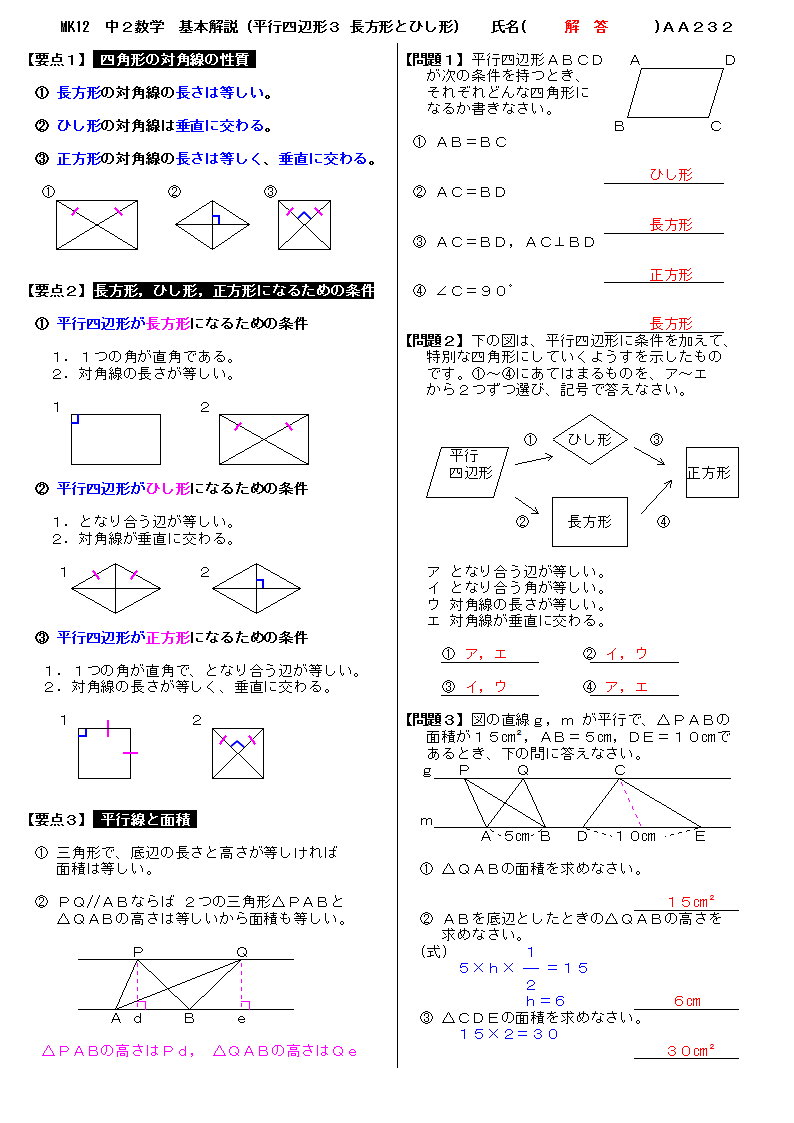
無料 中２数学 基本解説 解答プリント 232 平行四辺形３ 長方形とひし形

平行四辺形の定義 定理 性質 と証明問題 中学数学の図形 リョースケ大学

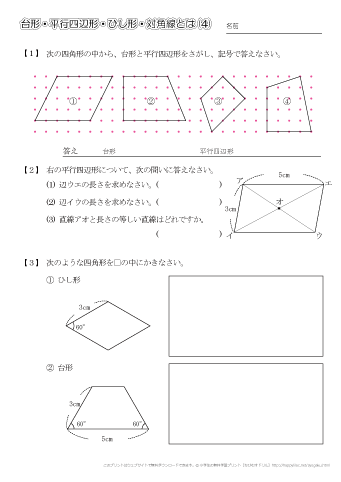
小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

平行四辺形の辺や角を求める Youtube

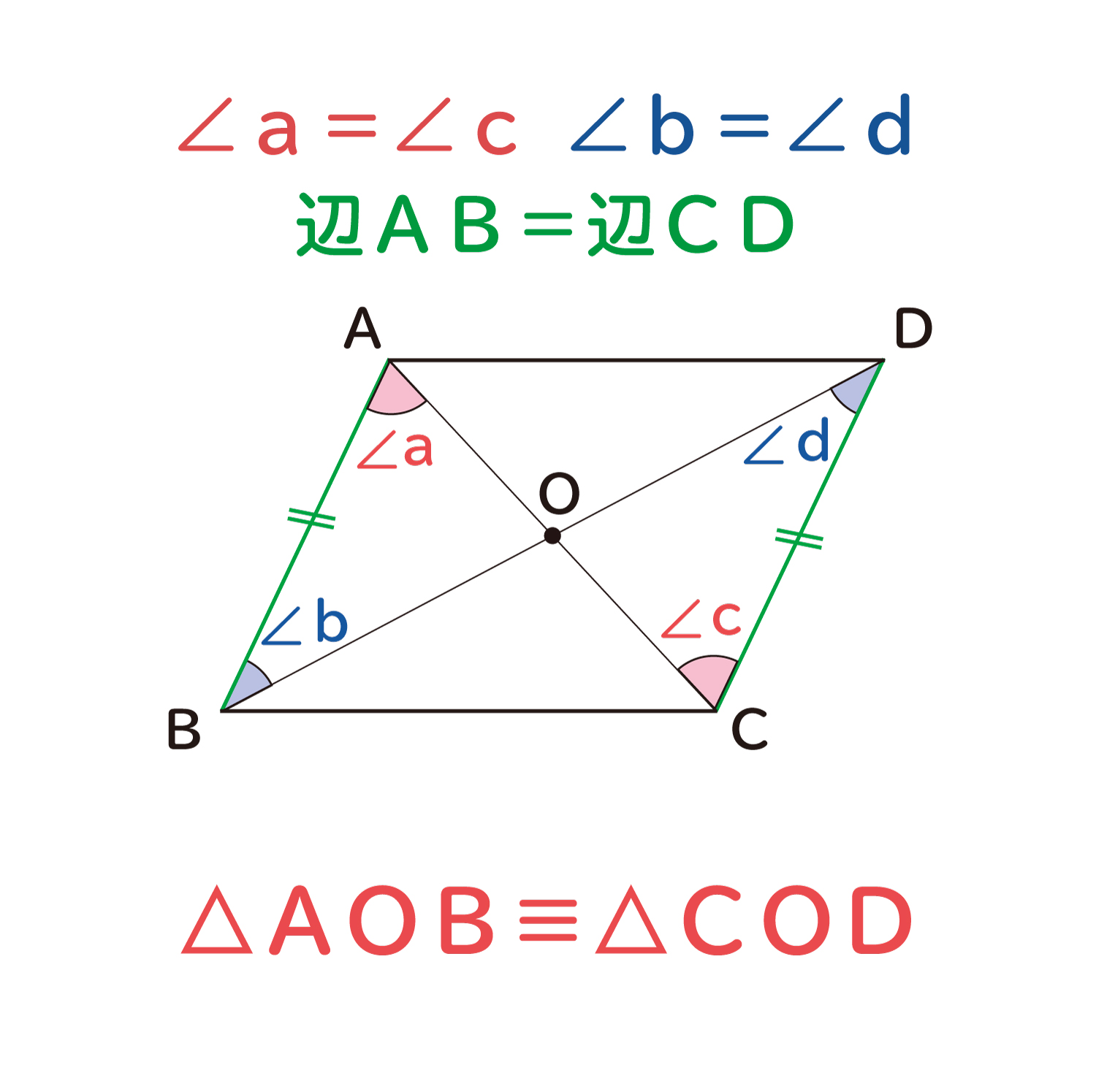
平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル

平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典

無料 中２数学 テスト対策 解答プリント 216 図形と合同４ 平行四辺形

平行四辺形の定義や性質を解説 面積の公式 証明問題も 受験辞典

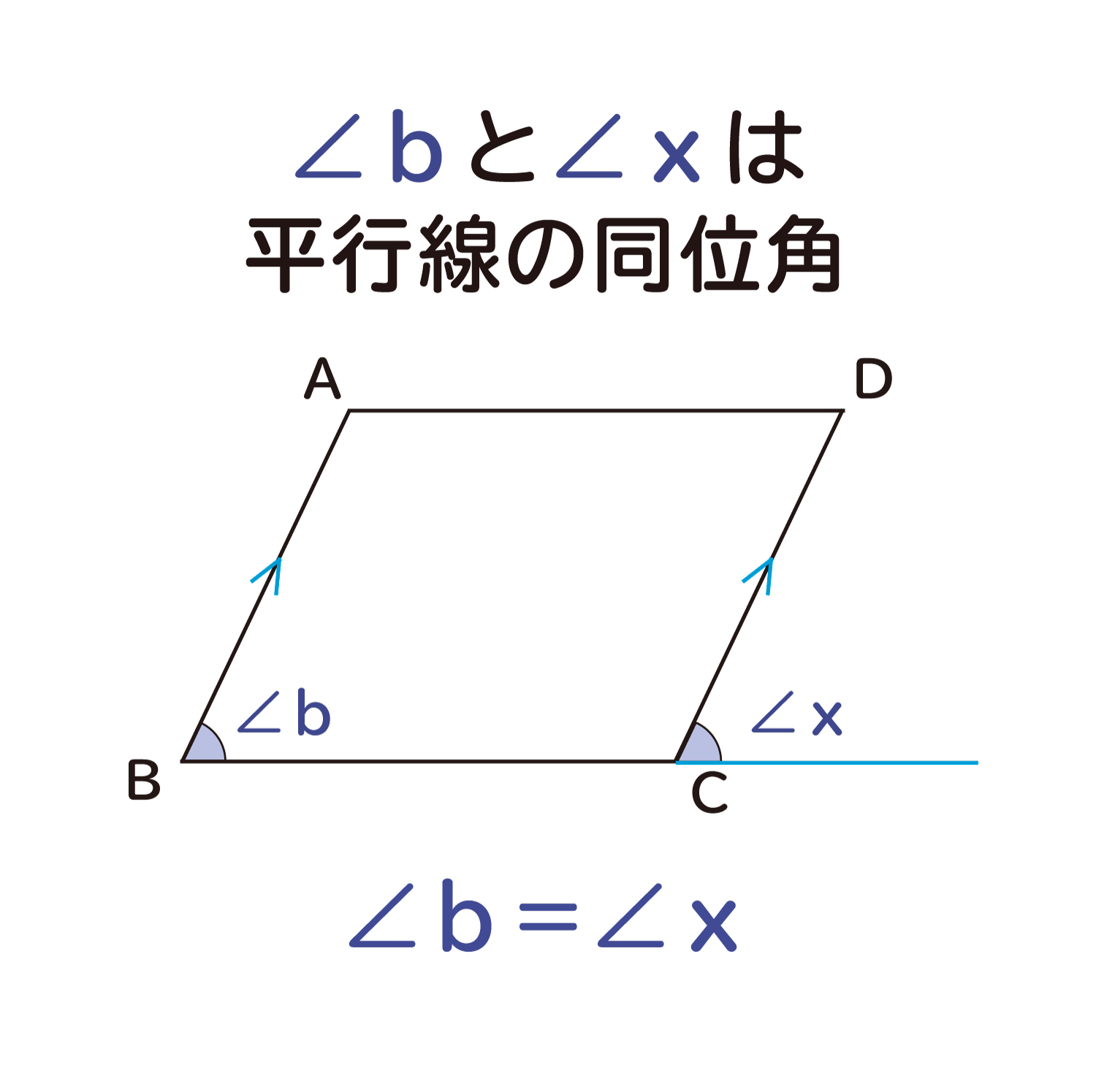
平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル

算数 小4 19 四角形の特ちょう Youtube

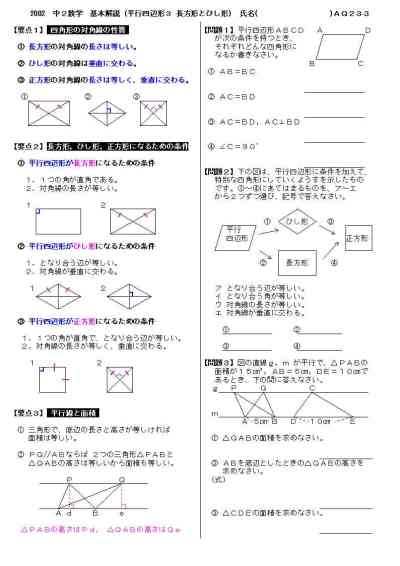
中２数学 基本解説 問題 233 平行四辺形３ 長方形とひし形 プリント

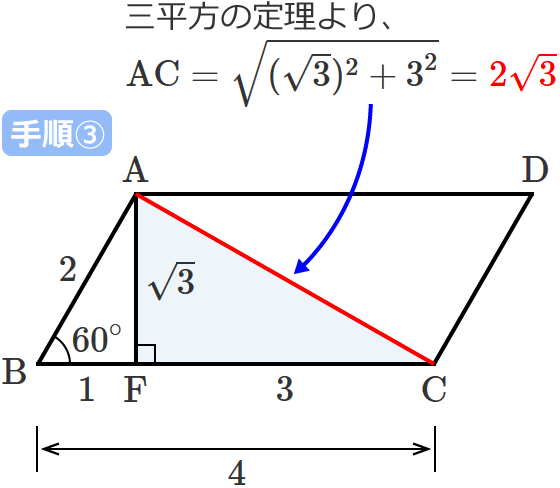
平行四辺形の対角線の長さの求め方

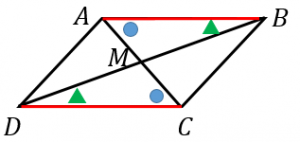
平行四辺形の3つの性質とその証明 具体例で学ぶ数学

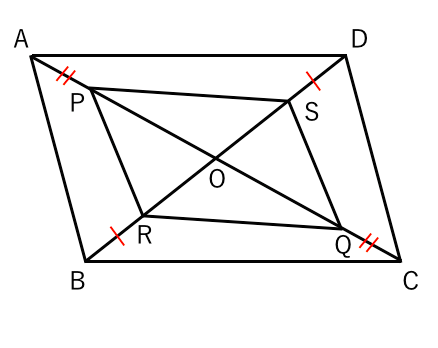
平行四辺形であることを証明する 苦手な数学を簡単に

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

高校数学b ベクトルの成分表示と平行四辺形 受験の月

平行四辺形の性質の利用２

小学４年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生

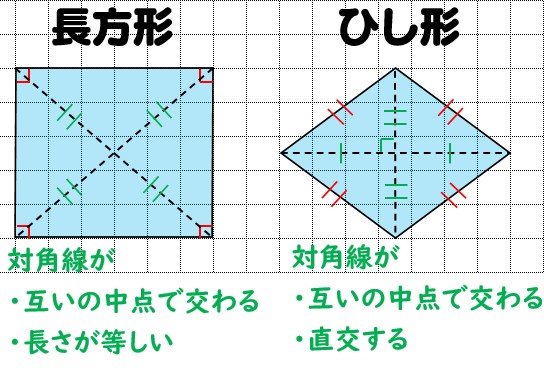
四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

平行四辺形の性質

四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun

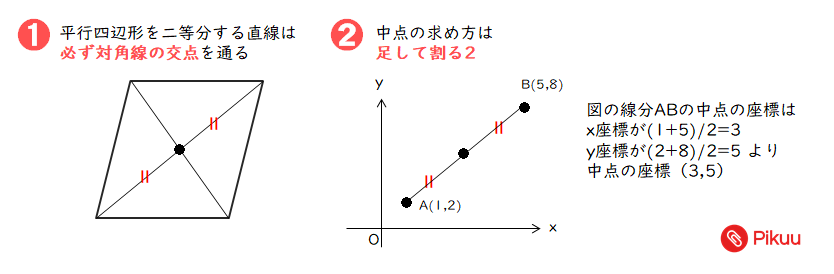
中学数学 平行四辺形の面積を二等分する直線を求める定期テスト予想問題 Pikuu

四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ

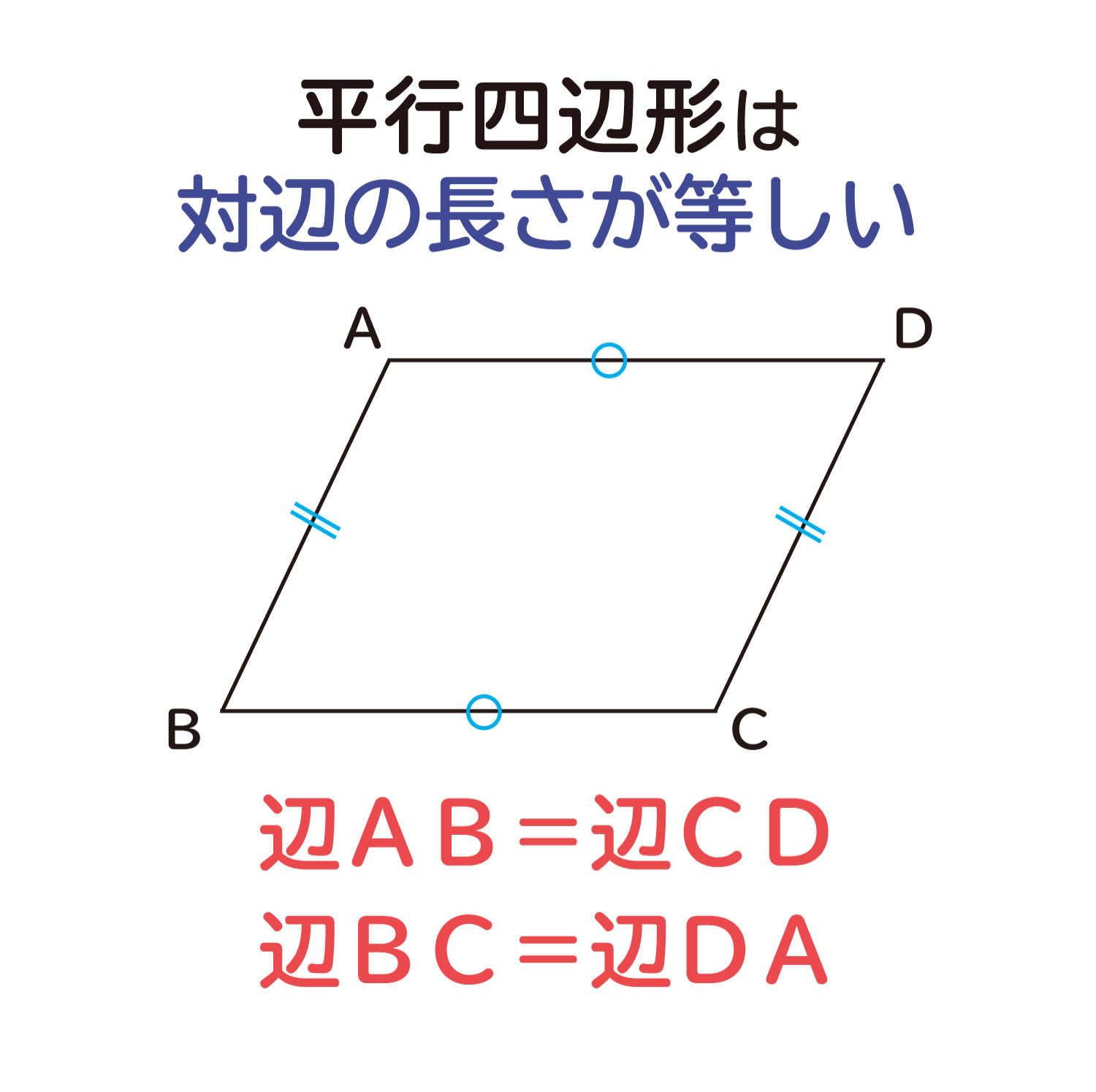
平行四辺形の対辺の長さは等しくなる ことの説明 おかわりドリル

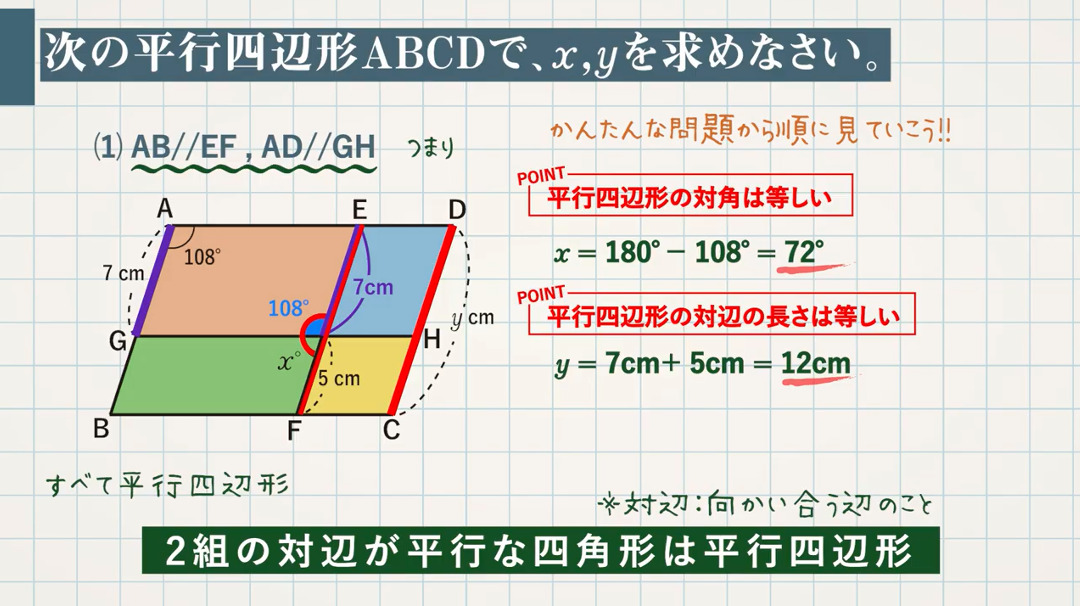
平行四辺形 二等辺三角形の辺の長さと角 応用問題まとめ 教遊者

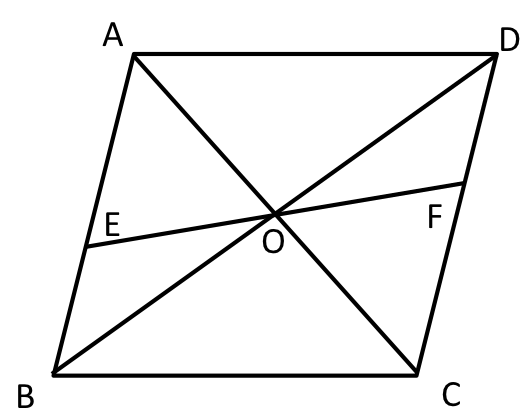
フロー 2 5 5 2 平行四辺形の性質を利用した証明

中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット

平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は４つ 中学や高校の数学の計算問題

平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく

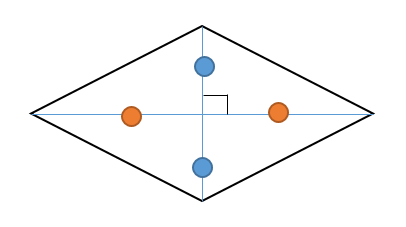
小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー

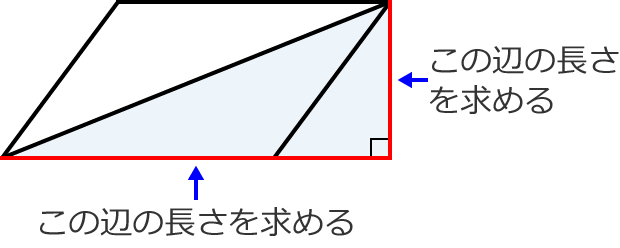
平行四辺形の対角線の長さの求め方

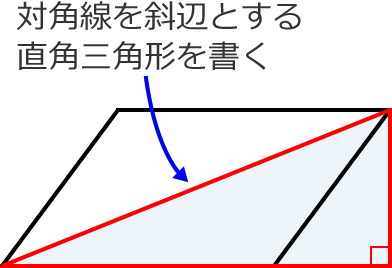
平行四辺形の対角線の長さの求め方

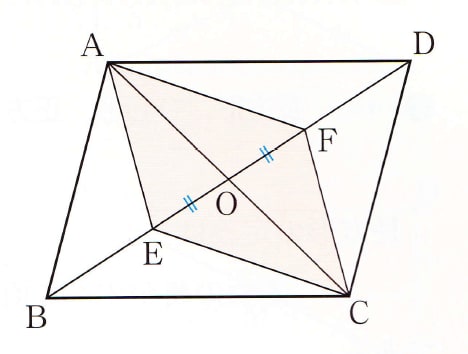
証明 は と が Takapの数学日記

中2 平行四辺形の性質 日本語版 Youtube

いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材

Incoming Term: 平行四辺形の対角線の性質,